2的平方根，2的平方根有啥？

2的平方根有啥

2的平方根有正负根号2

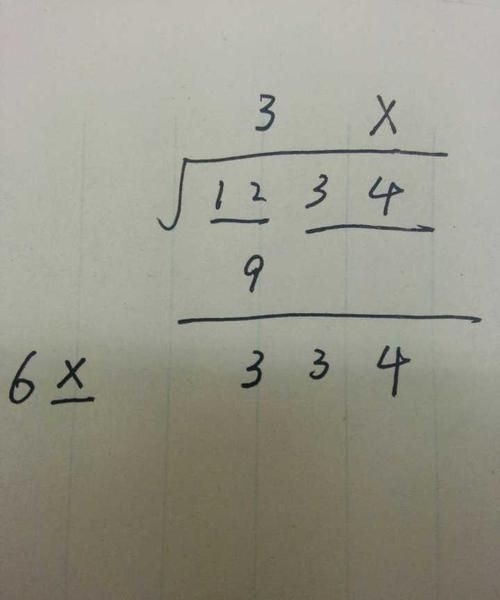
2的算术平方根是多少分数

2的算术平方根不能化成分数。理由如下：实数包括有理数和无理数，有理数包括整数和分数，整数包括正整数零和负整数，分数包括正分数和负分数。无理数是无限不循环小数。根据算术平方根的定义：2的算术平方根是根号2，根号2是无限不循环小数，是无理数，不能化成分数。

2的平方根是多少怎么算的

x²=2

x=±√2(√2≈1.414)

2的算术平方根约等于多少(精确到十分位)

2的算术平方根是1.4

~回答完毕~

~(^o^)/~祝学习进步~~~

2的算术平方根是多少

1.4142135623731 约等于1.414

它不能表示成两个整数之比，是一个看上去毫无规律的无限不循环小数。

2的算术平方根，俗称“根号“2”，记作√2，√ 在数学上称作“根号”，表示求一个数的算术平方根。数a的算术平方根记作√a，其中a≥0。例如，因为2²=4，所以√4=2。

0的算术平方根是0，而负数没有算术平方根。

能是最早被发现的无理数。相传毕达哥拉斯学派的希帕索斯首先提出了根号不是有理数的命题：若一个直角三角形的两个直角边都是1，那么它的斜边长，无法用整数或分数表示。

2的平方根到10的根分别是多少

2的平方根到10的平方根分别是多少？

这是一道让你写出2的平方根到IO的平方根分别是多少？

我们知道正数的平方根都是一对，它们是互为相反数。∴2的平方根到IO的平方根分别是：士根号2，士根号3，士2，士根号5，士根号6，土根号7，士2倍根号2，士3，士根号1O。（当然也可笔算开平方保留4个有效数字）。

2没有算术平方根对吗

答：2有算术平方根。

算术平方根：一般地说，若一个非负数x的平方等于a，则x叫做a的算术平方根。

中文名：算术平方根

外文名：arithmetic square root

学科：数学

符号：√

性质：双重非负性

如果x=√a，那么：1.a≥0（若小于0，则为虚数）；2.x≥0

与平方根的关系：正数的平方根有两个，它们为相反数，其中非负的平方根，就是这个数的算术平方根。负数没有算术平方根。

2的算术平方根是√2。

2的开方是多少怎么笔算

回答：2的开方，也就是2的平方根，2的算数平方根是√2≈1.414

2的开方怎么解

√2=1.4142135623730950488016887242097……

可以用计算器算，也可以用手算。只是手算麻烦一点而已。具体步骤如下：

第一步：将被开方数的整数部分从个位起向左每隔两位划为一段，用撇号分开，分成几段，表示所求平方根是几位数；

第二步：根据左边第一段里的数，求得平方根的最高位上的数；

第三步：从第一段的数减去最高位上数的平方，在它们的差的右边写上第二段数组成第一个余数；

第四步：把求得的最高位数乘以20去试除第一个余数，所得的最大整数作为试商；

第五步：用商的最高位数的20倍加上这个试商再乘以试商．如果所得的积小于或等于余数，试商就是平方根的第二位数；如果所得的积大于余数，就把试商减小再试；

第六步：用同样的方法，继续求平方根的其他各位上的数．

2平方根公式怎么推导

2的平方根怎么算过程？

∵X²=2，

∴X=±√2，

∴2的平方根是±√2。

2的根号是多少怎么算

√2= 1.4142135623731 ……

√2 是一个无理数，它不能表示成两个整数之比，是一个看上去毫无规律的无限不循环小数。早在古希腊时代，人们就发现了这种奇怪的数，这推翻了古希腊数学中的基本假设，直接导致了第一次数学危机。

根号二一定是介于1与2之间的数。

然后再计算1.5的平方大小……也就是一个用二分法求方程x^2=2近似解的过程。

扩展资料

现代，我们都习以为常地使用根号(如 等)，并感到它来既简洁又方便。那么，根号是怎样产生和演变成这种样子的呢?

古时候，埃及人用记号"┌"表示平方根。印度人在开平方时，在被开方数的前面写上ka。阿拉伯人用 表示 。1840年前后，德国人用一个点"."来表示平方根，两点".."表示4次方根，三个点"…"表示立方根，比如，.3、..3、…3就分别表示3的平方根、4次方根、立方根。到十六世纪初，可能是书写快的缘故，小点上带了一条细长的尾巴，变成" √￣"。

1525年，路多尔夫在他的代数着作中，首先采用了根号，比如他写是2，是3，并用表示，但是这种写法未得到普遍的认可与采纳。

直到十七世纪，法国数学家笛卡尔(1596-1650年)第一个使用了现今用的根号"√"。在一本书中，笛卡尔写道:"如果想求n的平方根，就写作±√n，如果想求n的立方根，则写作³√n。"