几何原本的作者(几何原本适合几年级看)

几何原本适合五年级看，《几何原本》又称《原本》，是古希腊数学家欧几里得所著的一部数学著作。它是欧洲数学的基础，总结了平面几何五大公设，被广泛地认为是历史上最成功的教科书。

我们来了解一下《几何原本》这本书，这本书适合7-14岁的学生去学习。这是欧几里得的一部不朽之作，集整个古希腊数学的成果于一身。既是数学著作，也是哲学著作，并且第一次完成了人类对空间的认识。中国现代的基本术语出处就是来源于这本书，比如直角、三角形、角等等。汉译的最早是由意大利传教士利玛窦和明代科学家徐光启1607年完成。下面我们来看看两千多年前的数学中部分内容。

CA1、如何在一个已知直线上做一个等边三角形？？？

图1.1

（1）分别以A、B两点为圆心，AB、BA为半径来画圆BCD和圆ACE。如图1.2所示

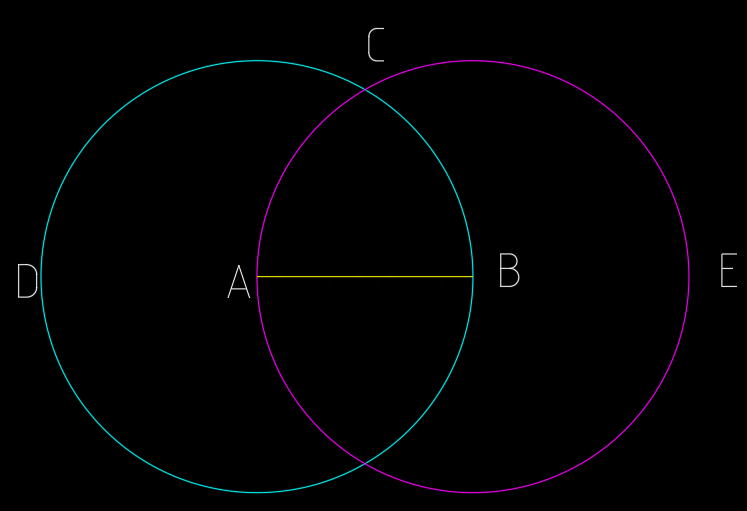
图1.2

（2）从两个圆的交点C到A、B，连接CA、CB。如图1.3所示[公设1：有任意一点到另外任意一点可以画直线]

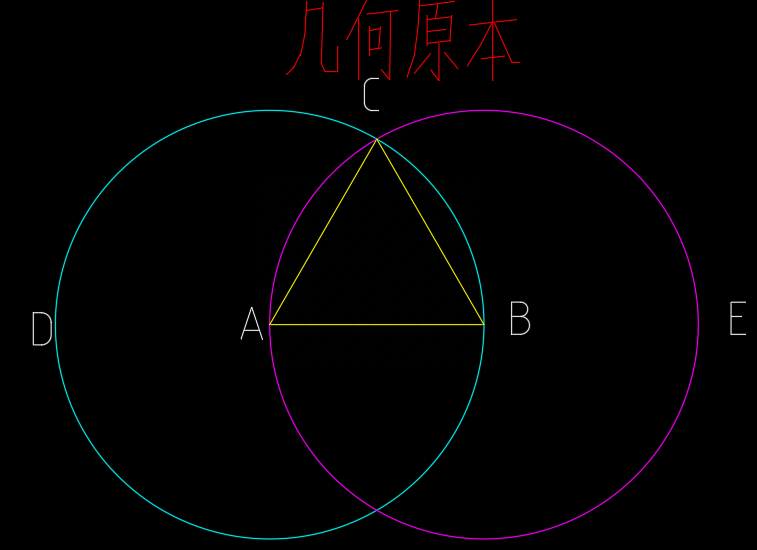
图1.3

2、如何证明黄色部分为等边三角形？

因为点A是圆CBD的圆心，所以AC等于AB。[定义15：圆是由一条线围成的平面图形，其内有一点与这条线上的点连接成的所有线段都相等]

又因点B是圆心CAE的圆心，因此BC等于BA[定义15：圆是由一条线围成的平面图形，其内有一点与这条线上的点连接成的所有线段都相等]

且由上已经证明了AC等于AB，因而线段CA、CB、都等于AB。且等于同量的量相等。[公里1：等于同量的量彼此相等]

综上得：三角形ABC是等边三角形，也就是在已给出的有限直线AB上作出了等边三角形。

这也是命题所要求：将一个已知点，作一条线段已知的线段。

证毕。

虽然这是两千多年前的内容，但是却将它延续到现代的教育中。证明中所运用的数学方法和思想，是我们现代人应该去继承和发扬的。